1Win bukmeker kontoru 2018-ci ildə yaradılıb. 2018-ci ilə qədər bukmeker kontoru FirstBet brendi altında mərcləri qəbul edirdi. 2020-ci ildə 1Win Azərbaycanda məhşurluq qazandı. 1win idman mərclərini qəbul edir, 3000 kazino oyunu, poker və onlayn kinoteatr təklif edir. Bütün xidmətlər bir oyun hesabı ilə bir yerdən mövcuddur. Filmlər onlayn kinoteatrda yalnız rus dilində nümayiş etdirilir.
2022-ci ildə qazanılan 1win bonusu bütün bukmeker kontorları arasında ən böyüyüdür. Yeni oyunçular 1680 AZN-ə qədər pul qazana bilərlər. Bonus böyükdür, lakin mərc tələbləri çətindir. Oyunçu bonus hesabından əmsalı 3 və ya daha çox olan hər mərcdən 5% alır.
2021-ci ildə 1win məşhur 1win aviator oyununu təqdim etdi

1win AZ- in rəsmi saytı
1win vahid rəsmi internet ünvanı yoxdur. İşi sürətləndirmək və provayderlər tərəfindən mümkün blokdan qorunmaq üçün yaradılmış bir çox domenlər var. Bu domenlərə 1win bet güzgüləri deyilir.
Saytın bütün bölmələri əsas menyuda mövcuddur. Burada bu linklər yerləşir:
- Xətt (tədbir başlamazdan əvvəl mərclər);
- Live (matç zamanı mərclər);
- Kazino;
- Live-games (canlı dilerlərlə qumar oyunları);
- ESports;
- Poker;
- Digər bölmələr.
Yuxarı sağ küncdə qeydiyyatdan keçmək və şəxsi hesabınıza daxil olmaq, həmçinin dil seçmək üçün düymələr var. Sayt Azərbaycan və digər 18 dildə fəaliyyət göstərir. Mobil proqramları yükləmək üçün düymələr də var. 1win-in Windows üçün proqramı var.
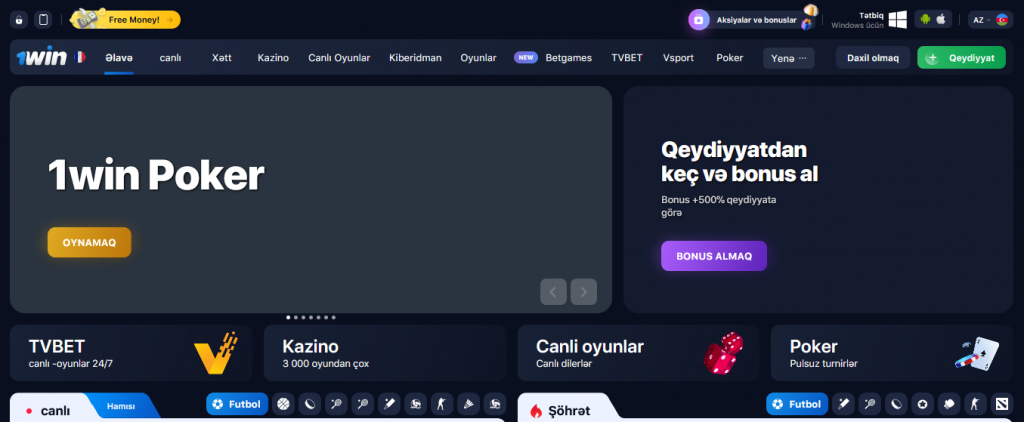

1win veb saytının əsas səhifəsində həmişə yeni və mövcud müştərilər üçün cari aksiyalar haqqında məlumat var.
Məlumatların əksəriyyəti yalnız qeydiyyatdan keçmiş istifadəçilər üçün əlçatandır. Bununla belə, bütün ziyarətçilər saytın funksionallığını qiymətləndirə bilər.
1win - də idman mərcləri
İdman mərcləri 1win azerbaycan əsas istiqamətidir. Buna baxmayaraq 1win az, idman mərclərində 1xbet, Parimatch, Melbet kimi böyük rəqiblərə uduzur
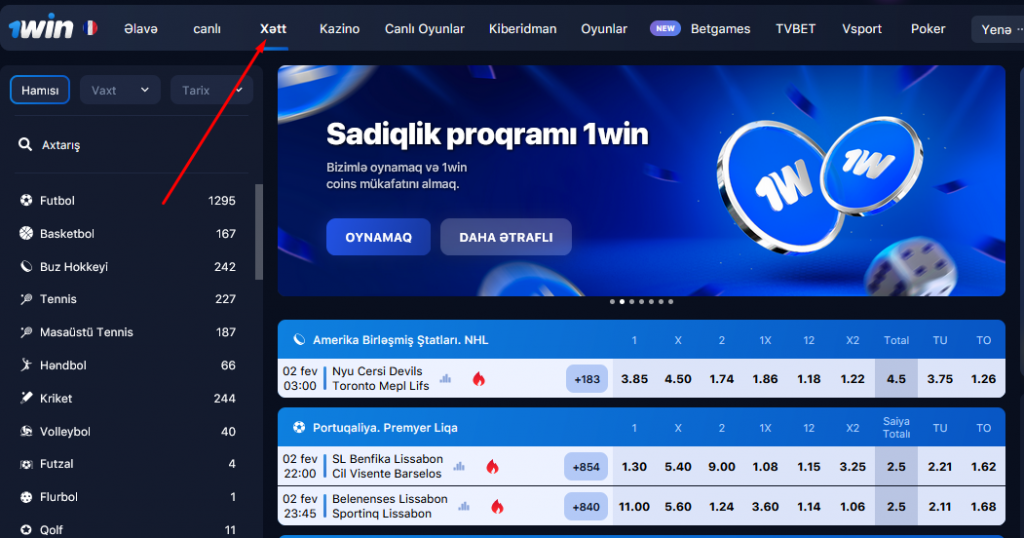
Xətt
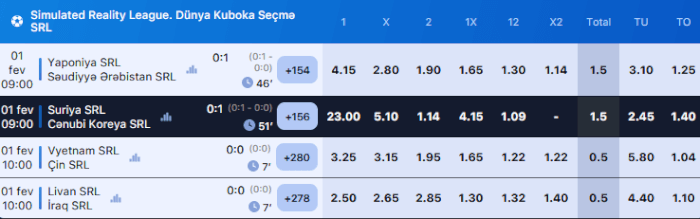
“Xətt” bölməsində mərclərin qəbul olunduğu qarşıdakı oyunlar təqdim olunur. Oyunçuların 20 klassik idman növünə (futbol, xokkey, basketbol, tennis), 6 eSport növünə (Counter-Strike, League of Legends, Dota 2, StarCraft, Call of Duty, FIFA) və eksklüziv xəttə (Qızıl buts, Eurovision qalibi və s.) mərcləri mövcuddur.
Tədbirlər idman, ölkələr, liqalar və çempionatlar üzrə sıralanır. Uyğun oyunların axtarış funksiyası mövcuddur. Siz müəyyən bir tarix və növbəti bir neçə saat üçün uyğun oyunları seçə bilərsiniz.
İstədiyiniz oyunu seçməklə, ona edə biləcəyiniz bütün mərc seçimlərini görəcəksiniz. Məşhur futbol oyunlarına 1000-ə qədər müxtəlif nəticələr daxildir. Ekzotik liqa matçları (məsələn, Ekvador ikinci liqası) 50-100 mərc seçimi təklif edir.
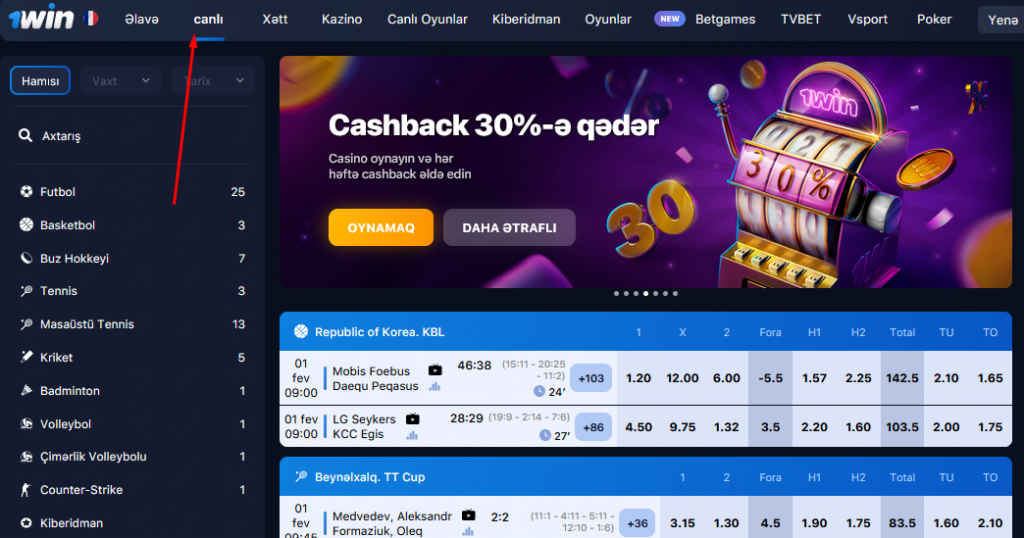
LIVE 1win Azerbaycan
“Live” bölməsində siz hazırda davam edən oyunları tapa bilərsiniz. Canlı mərclərə oyundaxili mərclər də deyilir. Adətən, canlı mərclərin müxtəlifliyi daha azdır və əmsallar “Xətt” bölməsinə nisbətən daha aşağıdır. Qarşılaşmada vəziyyət dəyişdiyi üçün əmsallar daim dəyişir. Bəzi mərclər yox olur və yeniləri görünür. Bütün bunlar yarışın dinamikasından asılıdır.
Statistikaya görə, mərclərin 80%-i Live rejimində edilir. Oyunçular oyun zamanı mərc etməyi xoşlayırlar. Bu mərclər daha tez hesablanır və oyuna baxarkən əlavə emosiyalar verir.
1win indir
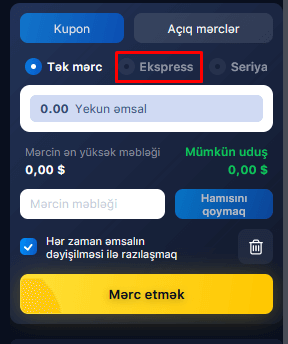
Ekspres mərclər
2 və ya daha çox seçimdən ibarət mərc “ekspress” adlanır. Hadisə əmsalları vurulur və yekun əmsalları əhəmiyyətli dərəcədə artırır. Müvafiq olaraq, mümkün qazanc artır. Məsələn, hər biri 1,8 və 2,3 əmsallarla 100 AZN-lik 2 mərc etsəniz, o zaman qalib gəlsəniz, 100*1,8+100*2,3=410 AZN və ya mərc məbləğinin 105%-ni (200 AZN) əldə edəcəksiniz. Əgər siz bu nəticələrdən ekspressə 100 AZN mərc etsəniz, o zaman qalibiyyət halında siz 100 * 1.8 * 2.3 = 414 AZN və ya mərc məbləğinin 314%-ni alacaqsınız. Ekspresə daha çox nəticə əlavə etsəniz, mümkün uduş məbləği daha da artacaq.
Ekspressin təhlükəsi ondadır ki, heç olmasa bir nəticənin itirilməsi halında bütün ekspress itirilir. Buna görə də, çoxlu nəticələrdən ekspresslər toplamamalısınız. Ekspress mərclər üçün daha az riskli nəticələri (kiçik əmsallarla, 1,6-a qədər) seçmək daha yaxşıdır. Mərc məbləğinə gəlincə, o, çox yüksək olmamalıdır, depozit məbləğinin 10%-dən çox olmamalıdır, hətta ondan da az olması daha yaxşıdır.
Əmsallar
İdman mərclərində 1win əmsalları çox yüksək deyil. Səbəb bukmeker kontorunun kifayət qədər yüksək komissiyasıdır (marja). Əmsalların ölçüsü, ilk növbədə, peşəkar oyunçular üçün vacibdir. Həvəskarlar üçün əmsallardakı fərq əhəmiyyət kəsb etmir. Uduşlarınızın 85% və ya 81% olacağının bir fərqi varmı?
Lakin əgər siz özünüzü peşəkar hesab edirsinizsə, onda bizim bukmekerlərin reytinqindən başqa bir bukmeker kontoru seçməyə cəhd edin.
Yayımlar 1 Win Bet
Saytda yayımların olması Live mərc həvəskarları üçün vacibdir. Canlı mərc edirsinizsə, hadisələrin real vaxtda necə cərəyan etdiyini görmək vacibdir. Tariflər və yayımlar bir yerdə olduqda rahatdır.
1win saytında siz gündəlik bir sıra yayımlar tapa bilərsiniz. Amma yayımların sayına görə 1win rəqiblərindən xeyli geri qalır. 1xbet, Melbet, Pin-Up saytlarında daha çox oyunlar yayımlayır.
Onlayn yayımla müşayiət olunan matç TV simvolu ilə qeyd olunur. Oyunu açdığınız zaman yayımı ayrıca pəncərədə görəcəksiniz. İstəsəniz, yayımı tam ekranda aça bilərsiniz.

Kazino 1 Win Az
Kazino bölməsi inanılmaz dərəcədə müxtəlifdir. Burada 3000-dən çox əyləncə tapa bilərsiniz. Oyunlar növlərinə (rulet, slot, stolüstü oyunlar, lotereyalar və s.), yenilik və populyarlıq üzrə çeşidlənir. Ulduz işarəsinə klikləməklə sevimli oyunlarınızı sevimlilərinizə əlavə edə bilərsiniz. Daha sonra yalnız seçdiyiniz oyunların göstəriləcəyi bölməyə sürətli şəkildə keçə biləcəksiniz.
Canlı dilerlərlə kazino oyunları ” Live-games” bölməsində qeyd olunur. Burada virtual slot maşınları ilə deyil, insanlarla oynayacaqsınız. Burada 80-ə yaxın əyləncə növü var.
TVBET mərc və stolüstü oyunlar arasında bir keçiddir. Burada siz nərd, poker, 21 xal və digər oyunlara mərc edə bilərsiniz.
1win Poker
Dünyanın ən məşhur kart oyununun pərəstişkarları birbaşa 1win saytında digər oyunçularla oynaya bilərlər. Minimum mərcləri 1 sentdən 10 dollara qədər olan oyunlar var. Həm təcrübəsiz oyunçular, həm də peşəkarlar öz səviyyələrinə uyğun rəqibləri burada tapacaqlar. 1win oyunların təşkilatçısı kimi çıxış edir. Poker oyunlarında iştirak haqqı hər əldə edilən uduşların faizi kimi tutulur. Adətən komissiya 5% təşkil edir.
Seçim kimi ” keş oyunlar ” və oyunçuların mükafat fondu üçün mübarizə etdiyi turnirlərdə mövcuddur.

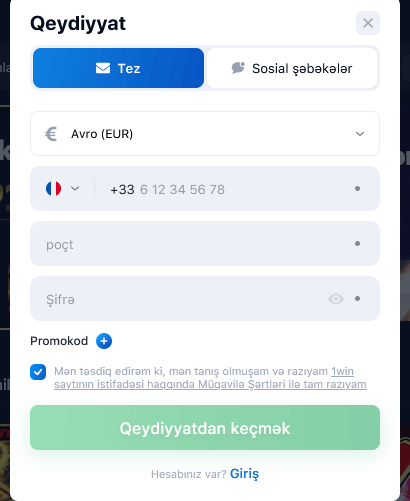
1win-də Qeydiyyat
Qeydiyyat proseduru 2 dəqiqə çəkir. Hesab açmaq üçün bir neçə seçim var:
- 1 kliklə;
- Telefon nömrəsi ilə;
- Sosial şəbəkələr vasitəsilə;
- E-poçt ünvanı ilə.
Qeydiyyatdan keçərkən ölkənizi və oyun hesabının valyutasını göstərməlisiniz. Adətən sistem özü uyğun variantı müəyyən edir. 2022-ci ilin əvvəlinə Azərbaycan manatı (AZN) daxil olmaqla 46 valyuta mövcuddur.
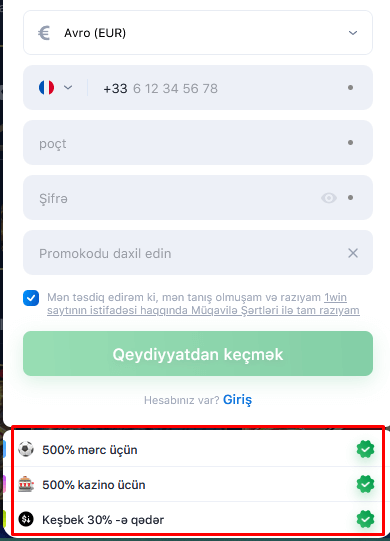
Qeydiyyat zamanı 1 win bonusu
1win azərbaycan bütün bukmeker kontorları arasında ən böyük qeydiyyat bonusunu verir. İlk depozit üçün 5 200 AZN-ə qədər əldə edə bilərsiniz. Bonus məbləği əmanətin 500%-ni təşkil edir. Hesabınızı 1 040 AZN-lə doldurun və bonus hesabınıza maksimum 5 200 AZN bonus qazanın.
Bonusun ölçüsünə aldanmayın. Bonusun mərc edilməsi şərtləri digər bukmeker kontorlarının promosyonlarından əhəmiyyətli dərəcədə fərqlənir. Bonusu geri qazanmaq olduqca çətindir, çünki yalnız 3 və ya daha çox əmsalı olan tək mərclər sayılır. Başqa sözlə, bonus pulu əldə etmək üçün yüksək risklə mərc etmək lazımdır.
Pulun yüklənməsi və çıxarılması
Aşağıdakı üsullarla oyun hesabınızı doldura və uduşlarınızı çəkə bilərsiniz:
- Visa və MasterCard kartları;
- Qiwi Elektron pul kisələri, Юмани və Webmoney;
- Payeer və Advcash ödəniş sistemləri;
- Kriptovalyutada (USDT və digər 17 növ).
Azərbaycanda oyunçular arasında ən populyar üsul bank kartlarıdır.
Hər bir metodun özünəməxsus limitlər və geri çəkmə müddətləri var . Adətən pul bir neçə dəqiqə ərzində hesaba daxil edilir, lakin bəzən bu proses bir günə qədər uzana bilər.
1win mobil tətbiqi indir
Mobil cihaz istifadəçiləri üçün 1win xidmətindən istifadə etmək üçün iki seçim var: mobil vebsayt və smartfonlar üçün mobil proqramlar. Mobil saytdan istifadə etmək üçün telefonunuzdan səhifənin yuxarısındakı linki izləmək kifayətdir. Proqramı Android və iOS üçün rəsmi 1win saytından yükləyə bilərsiniz.
Başqa bir yol, veb saytımızdan Android üçün 1win proqramını yükləməkdir. Aşağıdakı düyməni klikləməklə siz telefonunuza quraşdıra biləcəyiniz 1win.apk faylını endirəcəksiniz. Proqram PWA texnologiyası ilə işlədiyi üçün telefonun yaddaşında az yer tutur. Bu texnologiya mobil saytdan proqram kimi istifadə etməyə imkan verir. Klassik tətbiqdən bir qədər yavaş işləyir, lakin smartfonun yaddaşına qənaət edir. 1win yukle
1win az Texniki dəstəyi
1win müştəri dəstəyi 24/7 mövcuddur. Operatorla əlaqə saxlamaq üçün saytdakı söhbətdən istifadə edin. Problemləri səsli şəkildə həll etmək sizin üçün daha əlverişlidirsə, +7 495 088-88-99 nömrəsinə zəng edə bilərsiniz. Dəstək xidməti Moskvada (Rusiya) yerləşir, operatorlar rus dilində danışırlar.
1win dəstəyi ilə əlaqə saxlamağın üçüncü yolu contact@1win.xyz ünvanına e-poçt yazmaqdır. Bu mürəkkəb məsələləri həll etməyin ən yaxşı yoludur. Bütün digər suallarınız üçün saytdakı söhbətdən istifadə edin.
© 2023 1WIN. 1win.pro operated by 1WIN N.V. which is registered at Dr. H. Fergusonweg 1, Curaçao, with company number 147039, and having gaming license 8048/JAZ2018-040 and all rights to operate the gaming software. MFI INVESTMENTS LIMITED, a company, whose registered office is at 3, Chytron Street, Flat/Office 301, P.C. 1075 Nicosia, Cyprus with company number HE386738.EU company MFI Investments Ltd is providing payment services as an agent according to the license agreement concluded between MFI INVESTMENTS LIMITED and 1WIN N.V.



